Basics:
By TakalahTopics Covered
If you're in AP Chemistry, you can skip this part. This is the simple stuff, that I
will keep on adding to if the need may be, but I don't plan on this part being very big.
With that in mind, let's begin on the subject of what many of us are tested on first: Sig
Figs.
Significant Figures
In real life, you can't get a perfect measurement. Expensive and fancy instruments in
labs can measure things pretty accurately, but in high school you are stuck using rulers
and graduated cylinders. It's important to realize that fact, and you must record your
measurements accordingly. Here is an example:

You can see that you can't be sure whether it's 6.1489898 or 6.1501239223. The rule for
this is; get as many numbers you can be sure of, and then make an educated guess about the
last digit. So in this example, you can see it's definitely between 6 and 7, so you know
for sure the first number is 6. You can also see it's between the .1 and .2 marks, so you
know it's 6.1 for sure. But the next, and last digit is uncertain. It looks like the end
lies just around halfway between .1 and .2, so a safe guess is .05. Your final measurement
should be around 6.15, of which all numbers are significant figures.
(Note: If you need more examples, tell me. I don't know if some people need this
reinforced or something, that's all I plan to include on this.)
You'll need to know how many sig figs are in a measurement, to make proper
calculations. Here are some guidelines.
| Guidelines for Sig Figs Any number that isn't a zero is always a
sig fig.
Examples: 6.15 has three sig figs, 4.324 has 4 sig figs, 34231.123 has 8 sig figs, and
so on.
Zeros that don't have any non-zeros before them are not sig figs. They only act as
placeholders.
Examples: .00342 has only 3 sig figs, .02 has one sig fig, 02.3 has two sig figs, and
so on.
Zeros that are between two non-zeros (trapped) are always sig figs.
Examples: 100.02 has five sig figs, .0203 has only three (the first zero isn't,
according to Rule 2), 0101.00203 has eight sig figs, and so on.
Zeros that are at the end of the number are sig figs only if the number contains a
decimal point.
Examples: 123.00 has 5 sig figs, .003030 has 4 sig figs, 100. has three sig figs, (Note
that 100 by itself only has one sig fig, since it has no decimal) 2.30 x 10-16
has 3 sig figs, and so on.
Numbers in equations and conversions are considered to be exact, that is, have an
infinite number of sig figs.
Examples: In A = pr2, the 2 is exact. In 1 inch = 2.54 centimeters, 2.54 is
exact. |
|
When you do your calculations, you might naturally be
tempted to write as many numbers down as your calculator feeds, thinking that it is more
accurate. WRONG! Your accuracy of your answer can only be as precise as the numbers the
problems give you! For example, if a problem says something like this:
3.0 liters of water is added to 3.14159265358979323 liters of water. How
many liters of water are there?
The answer is not 6.14159265358979323. 3.0 liters means that the
actual value could be anywhere from 2.9 to 3.1 liters (remember the last number is just a
guess?). So with that much uncertainty, going all the way down to 3 x 10-12 liters doesn't
have as much an effect as the +/-0.5 that you have. The correct answer is 6.1 liters. How?
Here are a few simple rules governing the realm of sig figs:
To multiply or divide: You find the number with the least sig
figs, and use that many sig figs in the answer.
To add or subtract: The last digit in the final answer must have
the same place as the place of the least precise number. That is, the leftmost ending
value.
That's all there is to it. And just in case you forgot how to round
(something you should've learned in like fifth grade...)
Remember to finish all your addings and multiplyings, then round.
If the number to the right of where you're rounding to is 4 or less,
leave it alone and kill the numbers to right of it.
If the number to the right of where you're rounding to is 5 or greater,
add one to the number and kill the numbers to right of it.
Go try some SigFig practice now!
Prefixes
Instead of the annoying British system, with its gallons and quarts and pints and who
knows what, the SI system has an easier way of remembering how many small units go into
one big unit. It's the prefix system, and it's based on powers of ten. Makes it very
simple. Here is a table on some of the most commonly used prefixes:
Name of Prefix(symbol): |
Multiplier of Base |
Mega (M) |
106 |
Kilo (k) |
103 |
Hecto (h) |
102 |
Deka (da) |
101 |
--- |
1 |
Deci (d) |
10-1 |
Centi (c) |
10-2 |
Milli (m) |
10-3 |
Micro (m) |
10-6 |
Nano (n) |
10-9 |
|
So, some quick examples are: one kilometer is a thousand meters; one dekagram is a hundred
decigrams, and you can go on from there. These are only the most used prefixes; other ones
aren't used much in chem. Anyway, a more extensive list of prefixes will be included later
in the reference area.
Dimensional Analysis
Let's say that you have one unit, and need it in another unit. In other words, you need
to convert. A quick and easy way to do this is dimensional analysis. Basically, it uses
the concept of multiplying by one (where "one" is one unit divided by the
equivalence in another unit). Here's how to convert 100. meters into inches.
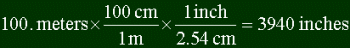
Note a few things. First, to convert you multiply your starting point with a series of
fractions to get the final answer. Each fraction is a unit over another, which are
equal. In the example, 100 cm is equal to 1 m, and 1 inch is equal to 2.54 cm. Thus
multiplying by one. The trick to figuring out what to put in each fraction is looking at
the units in the top of the previous fraction, and putting that unit in the bottom of the
next one. You look at meters in the top of the first fraction (it's 100. meters / 1), and
put that in the bottom of the next one. To figure out what unit to put in top, you look at
the final answer, and see if you can get a direct relation to it. Most people don't know
directly how many inches are in a meter, but it is common knowledge that there are 2.54 cm
in an inch. So perhaps converting into centimeters is a start...
Once you get the units right, plug in the numbers that make the top equal the bottom.
You should know that 100 cm's is an m. Now you go to the next fraction. cm's go in the
bottom, and you can go straight to inches, knowing the relation. You ultimately wants the
units converting to in the top of the last fraction. That way, everything cancels out, and
you're done.
Plugging the values in, and multiplying the fractions give you the answer.
Another couple of examples:
Converting 3.450 kg's into pounds.

Converting 434.2 atm's into torr:
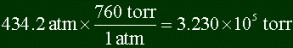
Usage of Periodic Table
You will be using the periodic table until your head explodes, so you'd better learn to
use it quick and efficiently from the beginning onward. I made a cool periodic table image
map that lets you click on an element, and gives info on it. Here is a section of it, and
what the number means.
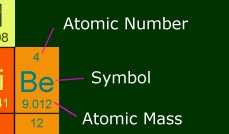
Atomic Number: This is how many protons are in the nucleus of one atom of this
element. It also shows the number of electrons in a stable atom of this element.
Symbol : This is the shorthand way of writing the element, and you will see it
like this in chemical equations.
Atomic Mass : This is the number you will be using the most during the AP test.
It is how much one atom weighs, in amus. 1 amu is 1 gram divided by Avogadro's number
(6.022 x 10-23). So in other words, one mole of beryllium has a mass of 9.012
grams. Anytime you need a molecular mass, you will be adding multiples of atomic masses.
Memorize some of the most common ones; it will save you some looking-up time.
For more info, visit the periodic table.
Copyright ©1999 by Takalah. All
rights reserved. This concepts portion was last updated on September 4, 1999